Maya Mathematics
Instead of ten digits like we have today, the Maya used a base number of 20. (Base 20 is vigesimal.) They also used a system of bar and dot as "shorthand" for counting. A dot stood for one and a bar stood for five.In the following table, you can see how this works.
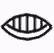 0 |
 1 |
 2 |
 3 |
 4 |
 5 |
 6 |
 7 |
 8 |
 9 |
 10 |
 11 |
 12 |
 13 |
 14 |
 15 |
 16 |
 17 |
 18 |
 19 |
Because the base of the number system was 20, larger numbers were written down in powers of 20. We do that in our decimal system too: for example 32 is 3*10+2. In the Maya system, this would be 1*20+12, because they used 20 as base.
Numbers were written from bottom to top. Below you can see how the number 32 was written:
| 20's |  (1) (1) |
| 1's |  (12) (12) |
It was very easy to add and subtract using this number system, but they did not use fractions. Here's an example of a simple addition:
| 8000's |  |  |  | ||
| 400's |  |  |  | ||
| 20's |  | + |  | = |  |
| 1's |  |  |  | ||
| 9449 | + | 10425 | = | 19874 |
As you can see, adding is just a matter of adding up dots and bars! Maya merchants often used cocoa beans, which they layed out on the ground, to do these calculations.
If you have a Java-enabled browser, you will see an interactive number converter below. Fill in the a number in the top field, and press return to find its Maya equivalent.. Press +1 and -1 to change the number by one.
Base twenty was also used in their calendar, which is a major portion of these pages because calendars are developed by astronomers for keeping track of time.
If you want to use the Maya number pictures shown above, you are free to do so provided you thank or credit me. Here is a zipped file containing the 20 GIF images (just 8.5k)